最小二乗法の事情（２）

マルチコ、もう少し状況を理解する

データモデリングの最も重要な手法である最小二乗法をもう一度見てみましょう。最小二乗法は、

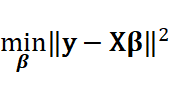
を満たすベクトル$\hat{\beta}$を求めることでした。ここで求めた推定式が、変数$x_1,x_2$の間でマルチコが発生したとしましょう。このとき$x_1,x_2$の推定された係数${\hat{\beta}}_1,{\hat{\beta}}_2$にどんなことが起こっているかを観察しましょう。

話を簡単にするために、\( x_1,x_2 \)の間のマルチコ、すなわち線形関係は\( x_1=\alpha x_2 \)となっていたとしましょう（定数項は話を簡単にするために省きます）。

また、最小二乗法で推計されたモデルは、\( y=ax_1 \)だった、すなわち\( x_2 \)の係数はゼロだったとします（ここでも定数項がなくてラッキーの場合を考えます）。今は\( x_2 \)の係数はゼロですが、先ほどの\( x_1=\alpha x_2 \)という関係を用いると次のような操作をすることで、\( x_2 \)の係数をいくらでも復活させられるのです。

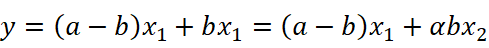
この式をよく観察すると、推計される係数\( {\hat{\beta}}_1,{\hat{\beta}}_2 \)は、\( {\hat{\beta}}_1+\frac{1}{\alpha}{\hat{\beta}}_2=a \)を満たしていれば、なんでもよい、ということになります。

ということで、係数\( {\hat{\beta}}_1,{\hat{\beta}}_2 \)は、ちょっとしたデータの揺れで大きくなったり、小さくなったり、この直線状をふらふらと揺れ動くことになります。さらに厄介なのは、今は二つの変数の関係でしたが、実際のデータでは複数の変数間で線形な関係が生じており、どこでマルチコが起こっているかすぐにはわからなかったりします。

極端な係数を抑え込む

　マルチコでは、変数間に線形な関係があり、先ほどの例のように係数の間にも線形な関係（直線的な関係）があることがわかりました。

推計モデルを安定させたい、ということは、極端に推計された係数があちこちに飛び出さない、ということでもありますので、マルチコ対策のために最小二乗法に係数制御のための評価関数を入れ込んでみようと思います。ここで\( \lambda \)は評価関数の重みづけになります。

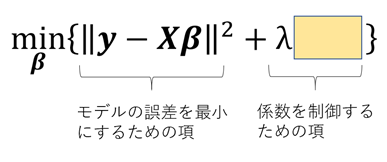
ちなみに、マルチコという現象は、モデルの精度が悪いわけではありません。誤差は限りなく小さくなるように推計をしているのですが、係数に自由度がありすぎてモデルが安定しない、という現象です。モデルの形を気にしないのであれば、実はあまり問題ではないとも言えます。

さて、ではどんな評価関数を入れていくかを考えましょう。やりたいことは直線の上を自由気ままに動かないでほしい、ある程度の範囲で動いてほしい、ということですから、一つのアイデアは「羽目を外さない」「極端な値を取らない」ということで、係数ベクトルのノルムをなるべく大きくしないようにする、となります。すなわち、

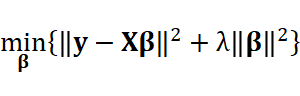
です。前半の誤差はほぼ最小化されているとすると、あとは後半のマルチコ部分を小さくすることになります。図示するとこのようなイメージです。

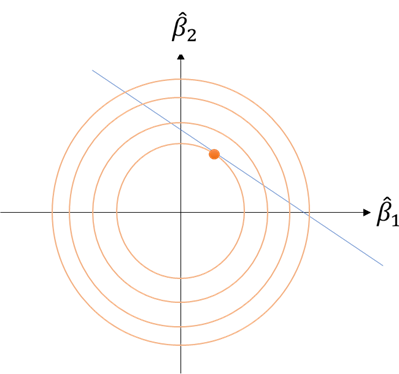
ここで観察してほしいのが、もしデータが多少揺れたとしても（すなわち直線の傾きとか切片が多少変化したとしても）、推計される係数はあまり変化がない、ということです。すなわち、推計されたモデルは、データが多少揺れても安定している、ということになります。

このように、最小二乗法に係数のノルム（\( l_2 \)ノルム）の補正を加えてマルチコ対策を行う手法をリッジ回帰(ridge regression)と呼びます [Amemiya, 1985]。うれしいことにこのリッジ回帰は最適解が陽に求めることが可能です。

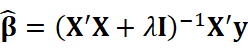
うまい具合に、もともとの最小二乗法の最適解の逆行列部分に\( \lambda I \)が入り込んだ数式です。逆行列が解ければ計算は容易です。

ノルムを変えてみてはどうか？

古典的な統計の教科書であればここで話は終わりますが、以前ロバスト回帰のお話をしたように、現代の計算機のスペックからすれば別に陽に最適解が求まらなくても数値計算でガンガン最適解を求めることができます。その観点からすると、係数を抑え込むノルムが\(l_2\)である必要はないような気がします。むしろ$l_1$ならどうか、と思うはずです。

　先ほどの図解を\(l_1\)で描いてみると、今度は$l_2$のように係数${\hat{\beta}}_1,{\hat{\beta}}_2$はお互いに仲良く分かち合うことはありません。${\hat{\beta}}_1,{\hat{\beta}}_2$のどちらかにぐっと寄って、もう片方は係数がゼロになります。この傾向は${\hat{\beta}}_1,{\hat{\beta}}_2$の直線の傾きが少し揺らいでも保たれます。（頭の中で角度を少し変えてみてください。多少動いてもl_1のひし形等高線の頂点が最適であることは変わりません…少しはずれますけどね。）

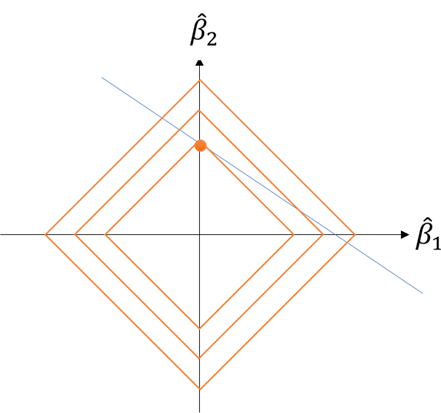
このように\( l_1 \)を用いた手法は、主要な変数を残して残りの変数をそぎ落とす効果があります。この性質は、変数がやたらと多いデータセットを扱うときに無駄な変数をそぎ落とすのに大変便利な性質と言えます。ビッグデータを扱う現代のデータサイエンスでは、この手法を発展させスパースエンジニアリングのモジュールとして各種分析システムに組み込まれています [岩波データサイエンス刊行委員会, 2017]。ちなみに、リッジ回帰の時と同じようにl_1を用いた回帰をラッソ回帰と呼びます。英語にすると、least absolute shrinkage and selection operator, LASSOです。

調子にのっていろいろなノルムを試してみるか？

ここまでくると、いろいろ試してみたくなります。いまは\( l_1 \)と\( l_2 \)を別のモデルにしましたけど、ええとこ取りするために二つを組み合わせてみたり、そもそも最小二乗法の部分もロバスト回帰みたいに別のノルムにしてもよいし…いろいろと想像は膨らみます。実際研究者はそういった試みをしています。より一般的には、回帰分析に係数の制御のための項を入れることを正則化(regularization)と呼び、こんな形をしています。

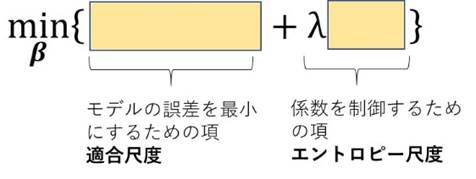
細かい話はここではしませんが、Wikipediaによれば少なくとも１０個くらいの組み合わせは過去に研究されているようです [Wikipedia, 2020]。

結局のところ答えは一つではない

マルチコに対する対応策として、リッジ回帰、ラッソ回帰などを見てきましたが、結局のところどれが良いかはモデルを使う人の都合に寄るということになります。

モデルが不安定になるのは確かにいろいろ都合が悪いのですが、推計されたモデルが悪いということは決してありません。さらにはラッソ回帰によって係数がゼロになった、としても、変数として意味がない、因果関係がない、というわけでありません。マルチコの場合、相棒となる変数に係数を寄せた（代理になってもらった）というだけです。驚くべきことに、係数が小さい・ゼロである、ということを短絡的に「無関係」と思い込む人は大変多いです。確かにマルチコがなければ無相関なのでしょうけど、そういったことを確認しないままモデルを解釈していることは現実には多くみられます。

データの時代と言いつつ、結構間違った理解も横行しているんですよね…とほほ

参照文献

AmemiyaTakashi. (1985). Advanced Econimetrics. Harvard University Press.

Wikipedia. (2020). 正則化. 
https://ja.wikipedia.org/wiki/%E6%AD%A3%E5%89%87%E5%8C%96
岩波データサイエンス刊行委員会. (2017). 岩波データサイエンス Vol．5 特集：スパースモデリングと多変量データ解析. 岩波書店