データの活用で直線のあてはめというのは様々なところに出てきます。何かを予測するとき、データ間の関係性を見るとき、目的はいろいろですが、ばらばらに獲得したデータの関係性を紐解いていくうえでまず直線であてはめてみるというのは定石です。その最も基本的な手法が、推計した直線と実際のデータの差(誤差)を最小にしようとする最小二乗法です。統計の教科書ならどこにでも出てくると思います。この最小二乗法を使うにあたり、困った現象についてお話したいと思います。
直線モデルをベクトル・行列で書く
今、予測したい値、すなわち目的変数を\(y\)とします。この目的変数を説明する説明変数は\(p\)個の変数から構成されるとします。すなわち、
\[ \textbf{x}=( x_1,x_2,\cdots ,x_K )’ \in R^K \]
とします。\(K\) は変数の個数です。(ここで\(‘\) はベクトルの転置です。)
直線は係数ベクトル
\[ \textbf{$\beta$}=( \beta_1,\beta_2,\cdots ,\beta_K )’ \in R^K\]
を用いて、
\[
y = \sum_{k=1}^{K}x_i \beta_i = \textbf{x}’ \textbf{$\beta$}
\]
となります。(フォントの問題で太文字になってませんが、\(\beta\)はベクトルです。)ここで、定数項はどこかの変数を\(x_i=1\) としておけばよいので、省略されています。(このあたりの細かいことは計量経済学の教科書に譲ることにします。)確認ですが、内積形式にするために\(\textbf{x}\) は転置されて横ベクトルとなります。
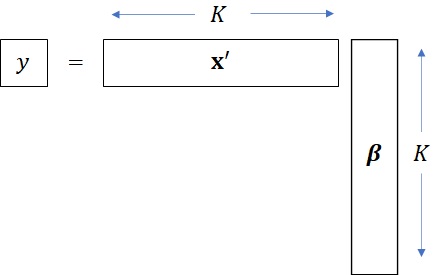
理論上のモデルが直線であっても、実際のデータには誤差が入り込みますから、どんなに近づけようとしても\(y\) と推計された\(\textbf{x}’ \textbf{$\beta$}\) の間には、誤差が生じます。(誤差がゼロになってしまうということは、逆に何か仮説が間違っていると思え!)誤差は右辺と左辺の差\(y-\textbf{x}’ \textbf{$\beta$}\) としてあらわされます。
さて、データを一気にベクトルと行列で表現します。全部で\(T\) 個のデータが得られたとします。そうすると\(y\) と\(\textbf{x}\) に相当する部分をベクトルと行列で表すと、以下のようになります。
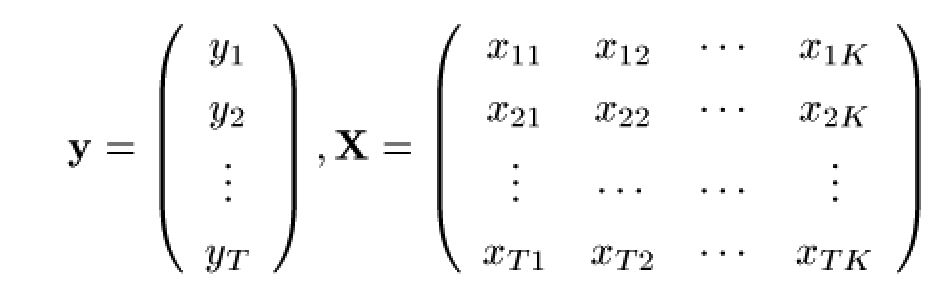
こちらの表記法は、主な計量経済学の教科書[1][2][3]などと同じですので、さらに勉強を進めるときに参考にしてください。(全部の統計の教科書を見たわけではないですが、時々行と列の書き方などが違いますので、注意してください。)
それぞれの大きさを、先ほどの箱で視覚的に表すとこのような感じです。
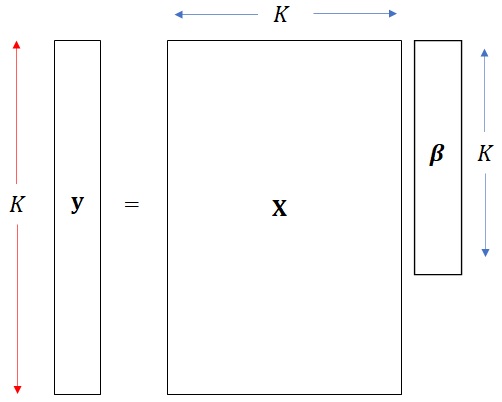
さて、データもベクトル・行列表記になったので、誤差もベクトル表記にします。
\[
\textbf{y} – \textbf{X}\textbf{$\beta$}
\]
この誤差ベクトルの大きさ、すなわちノルムを小さくするように直線の係数\(\textbf{$\beta$}\) を調整する、というのが直線モデル(線形モデル)の目標となります。
誤差ベクトルを最小化するような直線(線形モデル)を求めるということ、すなわち直線(平面)の係数\(\textbf{$\beta$}\) を求める問題を最適化問題風に書きますと以下のようになります。
\[
\mbox{min}_{\textbf{$\beta$}} \| \textbf{y} – \textbf{X}\textbf{$\beta$} \|
\]
なぜに、二乗?
ノルムはいろいろな種類があるという話は以前のブログで紹介しましたが、一番ポピュラーな\(l_2\) ノルムを採用した場合、このままの形よりノルムの二乗を最小化したほうが扱いが簡単なので、誤差の二乗を最小化する問題を解くことが一般的です。(求まる最適解は同じなので、扱いやすい方が良い、というだけです。)
最小二乗法とは、以下の問題の最適な\(\textbf{$\beta$}\) を求める問題として定式化されます。
\[
\mbox{min}_{\textbf{$\beta$}} \| \textbf{y} – \textbf{X}\textbf{$\beta$} \|_2^2
\]
ここで
\[
\| \textbf{y} – \textbf{X}\textbf{$\beta$} \|_2^2
=\sum_{t=1}^T \left( y_t – \textbf{x}_t’\textbf{$\beta$} \right)^2
\]
となります。
さて、この式、違和感を感じませんか?誤差を最小=誤差のノルムを最小、という解釈では良いのですが、なぜ二乗して足し算する\(l_2\) ノルムでなければならないのか?むしろ最小にするのは\(l_1\) ノルムだろ!すなわち、誤差の絶対値を足し合わせて、それが最小になった方が良いのではないか?
\[
\| \textbf{y} – \textbf{X}\textbf{$\beta$} \|_1
=\sum_{t=1}^T \left| y_t – \textbf{x}_t’\textbf{$\beta$} \right|
\]
こちらの方がストレートに誤差を小さくしているような気がしませんか?(こうやって、私は大学時代に、いらん詮索をして授業から脱落するのでした・・・)
話がそれましたが、最小二乗法が直線(線形モデル)推計に最も頻繁に用いられるのは、理由があります。私が思うに、以下の二つが重要だと思います。
1)最適解(推計値)が陽に数式として求まる。
ゆえに計算もしやすいし、推計値の性質もいろいろ確認できる。
2)理論的に「一番良い線形モデルの推計値である」とお墨付きがある。
より正確には、Best Linear Unbiased Estimator(BLUE、最良線形不偏推定量 )である。
ここでは統計的な準備は全くしていないので、BLUEについては深入りしませんが(興味ある方は[1 p.8][2 Ch.6])、乱暴に言いますと、「真のモデルのど真ん中を一目散に狙っている手法である、ということが保証される」のがBLUEという性質です。(まったく説明になっていないような気がしますが、統計学上素晴らしく正当性のある性質があると思っていただければ今は結構。)
最初の「推計値が陽に求まる」ということで言いますと、最小二乗法の最適解 \(\hat{\textbf{$\beta$}}\) は以下の式で求まります。
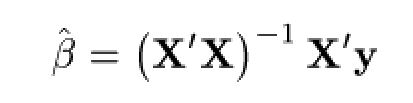
なるほど、これは便利です。逆行列の計算アルゴリズムさえできれば、あとはデータ行列の掛け算で済みます。
ちなみに、これを見て、ああ便利、と思えるのは自分で行列演算をプログラムしていたある程度のお年の方かも・・・学生時代の私は、自宅のパソコンで計量経済モデルのソフトを自作し計量モデルを作って楽しんでおりました。あー、懐かしい。
安定こそ、サラリーマンの夢
さて、統計的に素晴らしい性質の持ち主である最小二乗法ですが、実際にソフトを手に入れて遊び始めると、ある不具合に気づきます。あれ?データがちょっと変わると、推計モデルが全然変わってしまう・・・安定しない、と。症状・原因は大きく二つあります。
- データの測定ミス、入力ミスなどにモデルが踊らされる。
- データは正しく測定されているが変数間で係数を取り合いをして安定しない。
後者は、前回のブログで紹介したマルチコという問題になります。こちらの話をし始めるとまたまた時間がかかるので、今日は前者の問題まで言及したいと思います。
アウトライヤー退治
入力ミスや、予想外のノイズなどで、ほかのデータより大きく値がずれてしまうデータを、外れ値、アウトライヤー(outlier)と呼びます。入力ミスで桁が間違う、という場合は、ちゃんとチェックしろ!と言いたいところですが、本当に異常なことが起こってデータがほかのデータより突出してしまう場合もあります。
原因はいろいろありますし、場合によっては対処の方法(モデル、分析手法を変更するなど)もあります。
しかし、現実的には、異常がいつ起こるかわからないですし、ミスに気づかないこともあります。自動制御などにモデルを組み込む場合には、こういったアウトライヤーに対してあまり振り回されないような仕組みが求められます。少し硬い言い方をすると、実際に用いられる推計モデルには、多少の外れ値を含んでいたとしてもぶれない堅牢性(ロバスト性)を持つことが望まれます。
最小二乗法はとても便利で優秀な手法ではあるものの、外れ値に弱い傾向があります。それは、最小二乗法の最小化の式を再び見るとわかります。最小二乗法で最小化しようとしているのは、以下のような誤差の平方和です。
\[
\| \textbf{y} – \textbf{X}\textbf{$\beta$} \|_2^2
=\sum_{t=1}^T \left( y_t – \textbf{x}_t’\textbf{$\beta$} \right)^2
\]
一つの外れ値でも桁違いに大きいものが入ると、その二乗で評価関数がかく乱されます。例えば、誰かが千円と円の入力を間違うと3桁の二乗でデータが乱れちゃいます。やっぱり二乗にして足しこむと全体への影響が大きいんですよね。
そこで考えます。そもそも二乗である必要があるのか?というか、誤差の和を最小にするなら、二乗でなくて絶対値の和でよいのではないか?すなわち
\[
\| \textbf{y} – \textbf{X}\textbf{$\beta$} \|_1
=\sum_{t=1}^T \left| y_t – \textbf{x}_t’\textbf{$\beta$} \right|
\]
を最小化するようなモデルの方がアウトライヤーに強いのではないか?
答えは、Yes。この絶対値の和の最小化、もしくは\(l_1\)ノルムの最小化は最小二乗法とほぼ同じモデルを推計し、かつ外れ値に対して堅牢です。このようにモデル推計のための評価関数を工夫して堅牢性を持たせる回帰分析をロバスト回帰(頑健回帰)といいます。晴れて私が学生時代に思っていた疑問は晴れたのでした。直線のあてはめは、最小二乗法である必要はなく、時として別の誤差指標(ノルム)の方が良いこともあると・・・あとは克服すべきは、最小二乗法の美徳である
1)最適解(推計値)が陽に数式として求まる。
2)BLUEである。
の二つですが、2)のBLUEはあきらめざるを得ません。1)の計算についてですが、数学の公式として陽に求めるのは難しいのですが、計算アルゴリズムとしては現在では各種手法が適用可能だとわかっています。たとえば、少しテクニカルですが[4]を見ると\(l_1\) の場合の回帰分析について詳しい説明をしています。
さらには、今は\(l_2\) より\(l_1\) の方がロバストである話をしていますが、アウトライヤー対策ということであれば、あとから追加されたデータに対してもう少しゆっくり反応するようなノルムに近い誤差の和の関数も作れそうです。実際にそうなんです。そういったロバスト回帰に関するさらなる考察については、[5, p.144][6]などにあります。
今回は最小二乗法となぜ二乗なのか?もしくは二乗でない方がいいことはないか?ということでロバスト回帰についてお話しましたが、次回、気力があれば、さらにマルチコとの闘いについてお話できればと思います。
[1] Amemiya, T. (1985). Advanced econometrics. Harvard university press.
[2] Greene, H. W. (2000). Econometric Analysis, fourth ed. Printice-Hall, Englewood, Cliffs, NJ, USA.
[3] 浅野皙, 中村二朗. (2009). 計量経済学. 有斐閣.
[4] 末吉俊幸. (1997). 最小絶対値法による回帰分析. 日本オペレーションズ・リサーチ学会論文誌, 40(2), 261-275.
[5] 渋谷政昭, 柴田里程. (1992). S によるデータ解析.共立出版
[6] 「ロバスト回帰分析について」https://norimune.net/1775

No responses yet